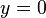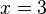2013 ~ Yudha Triya Blog

Minggu, 03 Maret 2013

Algoritma Menentukan Kemungkinan Rumus Umum Sebuah Barisan

17.55 1 comment

Keistimewaan tersebut cukup membantu dalam mencari kemungkinan dari bentuk umum sebuah barisan yang diketahui beberapa suku pertamanya. Langkah-langkah untuk mencari kemungkinan bentuk umum barisan tersebut salah satunya adalah:

Jika barisan tersebut (anggap barisan utama) adalah barisan konstanta atau dapat dianggap konstanta maka lanjutkan ke langkah terakhir.
Buat barisan selisih suku terus menerus sampai menghasilkan barisan konstanta atau dapat dianggap konstanta.
Hitung jumlah barisan selisih suku (misal ada q barisan), dan salah satu suku konstanta yang dihasilkan adalah p, maka dimungkinkan barisan utama tersebut mengandung komponen polinom : $\frac{p}{q!} n^q$ .
Hapus komponen polinom yang diperoleh dari langkah ke 3 dari barisan utama dengan mengurangi masing-masing suku barisan utama dengan nilai masing-masing suku komponen polinom yang diperoleh di langkah 3. Kemudian ulangi dari langkah 1 dengan barisan utama yang baru (setelah dihilangkan komponen polinom yang diperoleh dari langkah 3).
Kemungkinan rumus umum barisan yang kita cari adalah jumlah semua komponen yang diperoleh di langkah ke 3 ditambah salah satu suku barisan konstanta paling akhir (barisan utama baru terakhir).

Contoh Penggunaan Algoritma

Misalkan kita mencoba mencari salah satu kemungkinan rumus umum dari barisan bilangan 0, 0, 0, 6, ...

0, 0, 0, 6, .... bukan barisan konstanta maka,

0-0,0-0,6-0, ... atau 0, 0, 6, .... barisan selisih suku ke 1

0-0,6-0, ... atau 0, 6, ... barisan selisih ke 2

6-0, ... atau 6 ... barisan selisih ke 3 kita anggap barisan konstanta

ada 3 barisan selisih suku maka barisan utama mengandung komponen $\frac{6}{3!} n^3 = n^3$ .
Barisan n³ adalah 1, 8, 27, 64, ... kita hilangkan dari 0, 0, 0, 6, ... akan menghasilkan barisan 0-1,0-8,0-27,6-64,... atau -1, -8, -27, -58, ...
-1, -8, -27, -58, ... bukan barisan konstanta maka,

-8+1,-27+8,-58+27, ... atau -7, -19, -31, .... barisan selisih suku ke 1

-19+7,-31+19, ... atau -12, -12, ... barisan selisih ke 2 berupa barisan konstanta

ada 2 barisan selisih suku maka barisan utama mengandung komponen $\frac{-12}{2!} n^2 = -6n^2$ .
Barisan -6n² adalah -6, -24, -54, -96, ... hilangkan dari -1, -8, -27, -58, ... hasilnya -1+6,-8+24,-27+54,-58+96,... atau 5, 16, 27, 38, ...
5, 16, 27, 38, .... bukan barisan konstanta maka,

16-5,27-16,38-27, ... atau 11, 11, 11, .... barisan selisih suku ke 1 berupa barisan konstanta

ada 1 barisan selisih suku maka barisan utama mengandung komponen $\frac{11}{1!} n = 11n$ .
Barisan 11n adalah 11, 22, 33, 44, ... hilangkan dari 5, 16, 27, 38, ... hasilnya barisan 5-11,16-22,27-33,38-44,... atau -6, -6, -6, -6, ...
-6, -6, -6, -6, .... adalah barisan konstanta.

Kemungkinan rumus umum barisan 0, 0, 0, 6, ... adalah U_n = n³ - 6n² + 11n - 6

Manfaat Algoritma

Dalam kehidupan seringkali kita berusaha melihat keteraturan menjadi jelas dan dapat diprediksi. Data keteraturan yang dapat dinyatakan dengan bilangan dalam interval yang sama dengan kurun waktu tertentu akan membentuk sebuah barisan.

Barisan tersebut selalu mempunyai multi penafsiran untuk data-data yang belum terlampaui. Untuk menentukan kemungkinan pola keteraturan data tersebut sebagai alternatif prediksi dapat digunakan algoritme di atas.

Melalui algoritma ini dapat dengan banyak cara untuk mencari kemungkinan aturan suku suatu barisan, diantaranya

Menambah pada beberapa suku berikutnya

Misalnya ada barisan bilangan 2, 4, 6, .... maka kita dapat menentukan kemungkinan rumus umum barisan dengan tiga suku tersebut menggunakan algoritma.

Untuk mendapatkan kemungkinan yang lain kita dapat menambahkan beberapa suku berikutnya menggunakan bilangan yang kita kehendaki, misalnya untuk barisan tersebut dapat kita jadikan 2, 4, 6, 10, .... atau 2, 4, 6, 4, 2, .... dan masih banyak lagi.

Menyisipkan bentuk rumus umum yang diharapkan

Metode ini memungkinkan kita menyisipkan sembarang suku yang kita kehendaki.

Misal pada barisan bilangan 2, 4, 6, ..., jika kita menghendaki pada rumus umumnya terdapat suku n.sin(90n⁰) mak kita dapat mengambil bagian tersebut dari barisan 2, 4, 6, ..., sehingga muncul barisan 2-1.sin(90⁰), 4-2.sin(180⁰), 6-3.sin(270⁰), .... atau barisan bilangan 1, 4, 3, .....

Barisan 1, 4, 3, ... kita cari kemungkinannya menggunakan algoritma dan hasilnya dijumlahkan dengan n.sin(90n⁰).

Memecah masing-masing suku dengan aturan yang dikehendaki

Metode ini memecah masing masing suku dengan aturan yang sama, kemudian masing-masing pecahan suku kita buat barisan yang hasilnya kita gabung sesuai aturan pemecahan yang telah kita gunakan.

Misal 2, 4, 6, .... dapat kita pecah menjadi 1x2, 2x2, 2x3, ... sehingga muncul dua barisan yaitu 1, 2, 2, ... dan 2, 2, 3, .... Jika barisan pertama mempunyai rumus U_n1 dan barisan kedua memunyai rumus U_n2 maka rumus barisan 2, 4, 6, ... kemungkinan adalah U_n = U_n1.U_n2

Mengembangkan Algoritma

Keistimewaan yang telah ditunjukkan barisan polinom yang selalu memberikan barisan selisih suku ke derajatnya berupa barisan konstanta maka barisan selisih suku berikutnya adalah barisan 0 (nol).

Mengacu pada pengertian tersebut maka dengan meneliti perilaku barisan selisih suku disaat tanpa barisan polinom, kemungkinan akan mendapatkan keteraturan, sehingga memungkinkan membentukan algoritma berlandaskan keteraturan tersebut.

Dalam makalah seminar Menentukan Rumus Umum Barisan Polinom terdapat contoh algoritma untuk menyertakan sebuah suku eksponen dalam barisan polinom sebagai berikut:

Jika barisan tersebut (anggap barisan utama) adalah barisan konstanta atau dapat dianggap konstanta maka lanjutkan ke langkah terakhir.
Buat barisan selisih suku terus menerus sampai menghasilkan barisan dengan rasio sukunya sama atau rasio sukunya dapat dianggap sama.
Hitung jumlah barisan selisih suku (misal ada q barisan), dan nilai suku awal barisan selisih paling akhir adalah p, maka dimungkinkan barisan utama tersebut mengandung komponen suku eksponen : $\frac{p}{{(r-1)}^q} r^{n-1}$
Hapus komponen eksponen yang diperoleh dari langkah ke 3 dari barisan utama dengan mengurangi masing-masing suku barisan utama dengan nilai masing-masing suku komponen polinom yang diperoleh di langkah 3.
Jika barisan tersebut (anggap barisan utama) adalah barisan konstanta atau dapat dianggap konstanta maka lanjutkan ke langkah terakhir.
Buat barisan selisih suku terus menerus sampai menghasilkan barisan konstanta atau dapat dianggap konstanta.
Hitung jumlah barisan selisih suku (misal ada q barisan), dan salah satu suku konstanta yang dihasilkan adalah p, maka dimungkinkan barisan utama tersebut mengandung komponen polinom : $\frac{p}{q!} n^q$ .
Hapus komponen polinom yang diperoleh dari langkah ke 7 dari barisan utama dengan mengurangi masing-masing suku barisan utama dengan nilai masing-masing suku komponen polinom yang diperoleh di langkah 7. Kemudian ulangi dari langkah 5 dengan barisan utama yang baru (setelah dihilangkan komponen polinom yang diperoleh dari langkah 7).
Kemungkinan rumus umum barisan yang kita cari adalah jumlah semua komponen yang diperoleh di langkah ke 3 , dan 7, serta ditambah salah satu suku barisan konstanta paling akhir (barisan utama baru terakhir).

Misalnya kita mencari kemungkinan rumus umum barisan 2, 7, 24, 77, 238, ...

2, 7, 24, 77, 238, .... bukan barisan konstanta maka,

7-2,24-7,77-24,238-77, ... atau 5, 17, 53, 161, .... barisan selisih suku ke 1

17-5,53-17,161-53, ... atau 12, 36, 108, ... barisan selisih ke 2 kita anggap barisan mempunyai : $r = \frac{36}{12} = \frac{108}{36} = 3$

ada 2 barisan selisih suku dengan rasio 3 maka kemungkinan mengandung komponen $\frac{12}{{(3-1)}^2} 3^{n-1} = 3^n$ .
Barisan 3ⁿ adalah 3, 9, 27, 81, 243, ... kita hilangkan dari 2, 7, 24, 77, 238 ... akan menghasilkan barisan 2-3,7-9,24-27,238-234,... atau -1, -2, -3, -4, ...
-1, -2, -3, -4, .... bukan barisan konstanta maka,

-2+1,-3+2,-4+3, ... atau -1, -1, -1, .... barisan selisih suku ke 1 berupa barisan konstanta

ada 1 barisan selisih suku maka barisan utama mengandung komponen $\frac{-1}{1!} n = -n$ .
Barisan -n adalah -1, -2, -3, -4, ... hilangkan dari -1, -2, -3, -4, ... hasilnya barisan -1+1,-2+2-3+3,-4+4,... atau 0, 0, 0, 0, ...
0, 0, 0, 0, .... adalah barisan konstanta.

Kemungkinan rumus umum barisan 2, 7, 24, 77, 238, ... adalah $U_n = \frac{12}{{(3-1)}^2} 3^{n-1} = 3^n - n$ .

Melihat contoh di atas maka persoalan Deret aritmatika dan Deret ukur atau Deret Geometri memungkinkan juga dapat diselesikan menggunakan algoritma terakhir.

Membuat Barisan Polinom

17.48 No comments

Jika f sebuah fungsi polinom variabel tunggal maka barisan polinom yang dibangun dari fungsi f tersebut dapat dinyatakan dalam bentuk,
f(1) , f(2) , f(3) , .... , f(n) , .... mempunyai arti:

suku ke 1 = U₁ = f(1) suku ke 2 = U₂ = f(2) suku ke 3 = U₃ = f(3) ....................... suku ke n = U_n = f(n)	Barisan bilangan 0, 1, 3, 6, ... dapat diartikan, U₁ = 0 , U₂ = 1, U₃ = 3, U₄ = 6, .... , $U_n = \frac{1}{2} n^2 - \frac{1}{2} n$ atau barisan tersebut dibangkitkan oleh fungsi polinom $f(n) = \frac{1}{2} n^2 - \frac{1}{2} n$ berupa fungsi berderajat 2 Derajat polinom adalah pangkat tertinggi dari variabel fungsi polinom. Untuk i, a_i berupa bilangan cacah, $f(n) = a_i n^i + a_{i-1} n^{i-1} + \cdots + a_2 n^2 + a_1 n + a_0 =\sum\limits_{k=0}^{i}a_k n^k.$ maka fungsi f(n) mempunyai derajat i pada suku polinom a_inⁱ

suku ke 1 = U₁ = f(1) suku ke 2 = U₂ = f(2)
suku ke 3 = U₃ = f(3)
.......................
suku ke n = U_n = f(n)

Barisan bilangan 0, 1, 3, 6, ... dapat diartikan, U₁ = 0 , U₂ = 1, U₃ = 3, U₄ = 6, .... , $U_n = \frac{1}{2} n^2 - \frac{1}{2} n$ atau barisan tersebut dibangkitkan oleh fungsi polinom $f(n) = \frac{1}{2} n^2 - \frac{1}{2} n$ berupa fungsi berderajat 2 Derajat polinom adalah pangkat tertinggi dari variabel fungsi polinom.
Untuk i, a_i berupa bilangan cacah,

$f(n) = a_i n^i + a_{i-1} n^{i-1} + \cdots + a_2 n^2 + a_1 n + a_0 =\sum\limits_{k=0}^{i}a_k n^k.$

maka fungsi f(n) mempunyai derajat i pada suku polinom a_inⁱ

Menggali Keistimewaan Barisan Polinom

Dalam menggali keistimewaan barisan polinom kita mencoba membentuk beberapa pengertian sebagai jembatan untuk memperoleh beberapa keistimewaan tersebut.

Pengurangan Suku Barisan

Pengurangan Suku Barisan adalah hasil pengurangan suku barisan tertentu dengan suku sebelumnya. Sehingga pengurangan suku bisa dilakukan mulai suke ke dua.
Jika U_n merupakan rumus umum suku suatu barisan maka secara umum pengurangan suku dari barisan tersebut adalah U_n+1 - U_n.

Barisan Pengurangan Suku Barisan

Barisan Pengurangan Suku adalah barisan bilangan disusun dari pengurangan suku barisan suatu barisan.
Untuk mempermudah penulisan kita membuat simbol U^[i] untuk suku barisan pengurangan suku ke i.
Misalnya U_n suatu barisan maka barisan ini bukan barisan pengurangan suku dan khusus untuk ini kita sepakati sebagai U^[0]. Selanjutnya untuk n > 0,
U^[1] merupakan barisan pengurangan suku utama atau dari U sehingga U_n^[1] = U_n+1 - U_n U^[2] merupakan barisan pengurangan suku ke 1 atau dari U^[1] sehingga U_n^[2] = U_n+1^[1] - U_n^[1]
U^[3] merupakan barisan pengurangan suku ke 2 atau dari U^[2] sehingga U_n^[3] = U_n+1^[2] - U_n^[2]
...........................................
U^[i] merupakan barisan pengurangan suku ke i atau dari U^[i-1] sehingga U_n^[i] = U_n+1^[i-1] - U_n^[i-1]

Pengurangan Suku Barisan Polinom

Dengan mengambil i > 0 dan rumus umum barisan polinom,
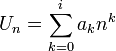
$U_n = \sum\limits_{k=0}^{i}a_k n^k$ maka Pengurangan Suku Barisan tersebut adalah
$U_{n+1} - U_n = \sum\limits_{k=0}^{i}a_k (n+1)^k - \sum\limits_{k=0}^{i}a_k (n)^k$ dengan menggunakan konsep sigma, kombinasi, dan binomial ^[3] diperoleh,
$U_{n+1} - U_n = \sum\limits_{k=0}^{i-1}a_k \sum\limits_{m=0}^{k-1} C^k_mn^m + a_i\sum\limits_{m=0}^{i-1}C^i_m n^m$

Barisan Pengurangan Suku Barisan Polinom

Dengan melihat persamaan terakhir pada pengurangan suku polinom tampak bahwa U^[1] mempunyai rumus umum sebagai berikut:
$U^{[1]}_n = \sum\limits_{k=0}^{i-1}a_k \sum\limits_{m=0}^{k-1} C^k_mn^m + a_i\sum\limits_{m=0}^{i-1}C^i_m n^m$ Tampak jelas bahwa barisan selisih suku pertama tersebut berupa barisan polinom. Derajat fungsi polinom dapat dilihat pada bagian
$a_i\sum\limits_{m=0}^{i-1}C^i_m n^m$ yaitu saat m = i-1 dan memberikan komponen polinom
$a_i C^i_{i-1} n^{i-1} = a_i i n^{i-1}$ berarti derajat fungsi polinom yang menyusun U^[1] adalah i-1 atau turun satu dari derajat fungsi polinom penyusun U. Koefisien suku fungsi polinom yang berpangkat i-1 dari penyusun U^[1] ternyata adalah koefisien suku fungsi polinom komponen yang berpangkat i dari penyusun U dikalikan derajat fungsi penyusun U atau sama dengan a_ii

Keistimewaan Barisan Polinom

Pada akhir penggalian keistimewaan barisan polinom dapat dengan mudah kita simpulkan adanya beberapa keistimawaan barisan polinom ^[4] tersebut yaitu:

Barisan selisih suku ke derajad polinom yang dibentuk akan berupa barisan konstanta.
Besar konstanta adalah ai!, dengan a koefisien suku yang berpangkat tertinggi dari fungsi yang membentuk barisan, dan i merupakan derajat fungsi polinom tersebut.

Notasi i! artinya faktorial dari i.

Barisan Polinomial

17.37 No comments

Barisan Polinomial adalah barisan bilangan^[1] yang dibentuk dari fungsi polinom ^[2] variabel tunggal dengan domain fungsi bilangan asli.
Beberapa peristiwa dapat memberikan data yang menggambarkan keberadaan barisan ini, misalnya data banyaknya jabat tangan yang terjadi pada sekelompok orang. Jumlah orang dalam kelompok sebagai urutan suku dan jumlah jabatan tangan dari mereka adalah nilai sukunya. Sehingga dapat dinyatakan dalam bentuk:

Jika ada 1 orang dalam kelompok maka tidak ada jabatan tangan
Jika ada 2 orang dalam kelompok maka hanya ada 1 jabatan tangan
Jika ada 3 orang dalam kelompok maka ada 3 jabatan tangan
Jika ada 4 orang dalam kelompok maka ada 6 jabatan tangan
dan seterusnya

Rangkaian bilangan di atas dapat dinyatakan dalam bentuk barisan: 0, 1, 3, 6, ... . Tentu akan menyulitkan kita jika ingin melihat jumlah jabatan tangan pada kelompok yang anggotanya 201 orang. Untuk itu seringkali kita berusaha mencari bentuk umum dari barisan tersebut, dan benar bahwa pada barisan tersebut apabila jumlah n orang dalam kelompok secara umum terdapat $\frac{n^2 - n}{2}$ atau $U_n = \frac{1}{2} n^2 - \frac{1}{2} n$ jabatan tangan yang menunjukkan barisan tersebut berupa barisan polinom.
Proses pencarian kemungkinan bentuk umum peristiwa di atas sering dipakai konsep kombinasi, tetapi ternyata prinsip-prinsip keistimewaan barisan polinom dengan menggunakan operasi aritmatika sederhana dari operasi pengurangan, penjumlahan, perkalian dan pembagian, juga dapat dimanfaatkan.

Persamaan Linear dengan Matriks

17.30 No comments

Persamaan linear dapat dinyatakan sebagai matriks. Misalnya persamaan:

3x₁ + 4x₂ − 2x₃ = 5

x₁ − 5x₂ + 2x₃ = 7

2x₁ + x₂ − 3x₃ = 9

dapat dinyatakan dalam matriks teraugmentasi sebagai berikut
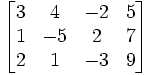
$\begin{bmatrix} 3 & 4 & -2 & 5\\ 1 & -5 & 2 & 7\\ 2 & 1 & -3 & 9\\ \end{bmatrix}$
Penyelesaian persamaan linier dalam bentuk matriks dapat dilakukan melalui beberapa cara, yaitu dengan eliminasi Gauss atau dapat juga dengan cara eliminasi Gauss-Jordan. Namun, suatu sistem persamaan linier dapat diselesaikan dengan eliminasi Gauss untuk mengubah bentuk matriks teraugmentasi ke dalam bentuk eselon-baris tanpa menyederhanakannya. Cara ini disebut dengan substitusi balik.
Sebuah sisitem persamaan linier dapat dikatakan homogen apabila mempunyai bentuk :

a₁₁x₁ + a₁₂x₂ + ... + a_1nx_n = 0

a₂₁x₁ + a₂₂x₂ + ... + a_2nx_n = 0

a_m1x₁ + a_m2x₂ + ... + a_mnx_n = 0

Setiap sistem persamaan linier yang homogen bersifat adalah tetap apabila semua sistem mepunyai x₁ = 0 , x₂ = 0 , ... , x_n = 0 sebagai penyelesaian. Penyelesaian ini disebut solusi trivial. Apabila mempunyai penyelesaian yang lain maka disebut solusi nontrivial.

Penyelesaian Persamaan Linear dengan Matriks

Bentuk Eselon-baris

Matriks dapat dikatakan Eselon-baris apabila memenuhi persyaratan berikut :

Di setiap baris, angka pertama selain 0 harus 1 (leading 1).
Jika ada baris yang semua elemennya nol, maka harus dikelompokkan di baris akhir dari matriks.
Jika ada baris yang leading 1 maka leading 1 di bawahnya, angka 1-nya harus berada lebih kanan dari leading 1 di atasnya.
Jika kolom yang memiliki leading 1 angka selain 1 adalah nol maka matriks tersebut disebut Eselon-baris tereduksi

Contoh:

syarat 1: baris pertama disebut dengan leading 1

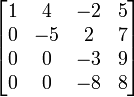
$\begin{bmatrix} 1 & 4 & -2 & 5\\ 0 & -5 & 2 & 7\\ 0 & 0 & -3 & 9\\ 0 & 0 & -8 & 8\\ \end{bmatrix}$

syarat 2: baris ke-3 dan ke-4 memenuhi syarat 2

$\begin{bmatrix} 1 & 4 & -2 & 5\\ 0 & -5 & 2 & 7\\ 0 & 0 & -3 & 9\\ 0 & 0 & 0 & 0\\ \end{bmatrix}$

syarat 3: baris pertama dan ke-2 memenuhi syarat 3

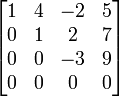
$\begin{bmatrix} 1 & 4 & -2 & 5\\ 0 & 1 & 2 & 7\\ 0 & 0 & -3 & 9\\ 0 & 0 & 0 & 0\\ \end{bmatrix}$

syarat 4: matriks dibawah ini memenuhi syarat ke 4 dan disebut Eselon-baris tereduksi

$\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix}$ $\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 2 & 5\\ 0 & 0 & 3 & 0\\ 0 & 0 & 0 & 6\\ \end{bmatrix}$

Operasi Eliminasi Gauss

Eliminasi Gauss adalah suatu cara mengoperasikan nilai-nilai di dalam matriks sehingga menjadi matriks yang lebih sederhana (ditemukan oleh Carl Friedrich Gauss). Caranya adalah dengan melakukan operasi baris sehingga matriks tersebut menjadi matriks yang Eselon-baris. Ini dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Caranya dengan mengubah persamaan linear tersebut ke dalam matriks teraugmentasi dan mengoperasikannya. Setelah menjadi matriks Eselon-baris, lakukan substitusi balik untuk mendapatkan nilai dari variabel-variabel tersebut.
Contoh: Diketahui persamaan linear

$x + 2y + z = 6$

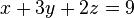
$x + 3y + 2z = 9$

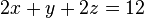
$2x + y + 2z = 12$

Tentukan Nilai x, y dan z
Jawab: Bentuk persamaan tersebut ke dalam matriks:

$\begin{bmatrix} 1 & 2 & 1 & 6\\ 1 & 3 & 2 & 9\\ 2 & 1 & 2 & 12\\ \end{bmatrix}$

Operasikan Matriks tersebut $\begin{bmatrix} 1 & 2 & 1 & 6\\ 1 & 3 & 2 & 9\\ 2 & 1 & 2 & 12\\ \end{bmatrix}$ B1 x 1 , Untuk mengubah a₁₁ menjadi 1
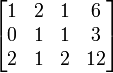$\begin{bmatrix} 1 & 2 & 1 & 6\\ 0 & 1 & 1 & 3\\ 2 & 1 & 2 & 12\\ \end{bmatrix}$ B2 - 1.B1 , Untuk mengubah a₂₁ menjadi 0
$\begin{bmatrix} 1 & 2 & 1 & 6\\ 0 & 1 & 1 & 3\\ 0 & -3 & 0 & 0\\ \end{bmatrix}$ B3 - 2.B1 , Untuk mengubah a₃₁ menjadi 0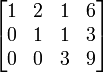
$\begin{bmatrix} 1 & 2 & 1 & 6\\ 0 & 1 & 1 & 3\\ 0 & -3 & 0 & 0\\ \end{bmatrix}$ B2 x 1 , Untuk mengubah a₂₂ menjadi 1
$\begin{bmatrix} 1 & 2 & 1 & 6\\ 0 & 1 & 1 & 3\\ 0 & 0 & 3 & 9\\ \end{bmatrix}$ B3 + 3.B2 , Untuk mengubah a₃₂ menjadi 0
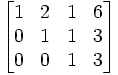$\begin{bmatrix} 1 & 2 & 1 & 6\\ 0 & 1 & 1 & 3\\ 0 & 0 & 1 & 3\\ \end{bmatrix}$ B3 x 1/3 , Untuk mengubah a₃₃ menjadi 1 (Matriks menjadi Eselon-baris)
Maka mendapatkan 3 persamaan linier baru yaitu

$x + 2y + z = 6$

$y + z = 3$

$z = 3$

Kemudian lakukan substitusi balik maka didapatkan:

$y + z = 3$

$y + 3 = 3$

$y = 0$

$x + 2y + z =6$

$x + 0 + 3 = 6$

$x = 3$

Jadi nilai dari $x = 3$ , $y = 0$ ,dan $z = 3$

Spurs Petik Kemenangan ke-33 di Musim Ini

17.19 No comments

PHILADELPHIA _ Tim Duncan mencetak double-double dan Tony Parker mengemas poin double digit untuk membawa San Antonio Spurs menaklukan Philadelphia 76ers 90-85 dalam lanjutan NBA. Ini merupakan kemenangan ke-33 Spurs musim ini.
Bertanding di Wells Fargo Center, Philadelphia, pemain veteran Duncan masih belum kehilangan tajinya. Power forward berusia 36 tahun ini membuat 24 poin dan 17 rebound.
Meski tak diperkuat shooting guard asal Argentina Manu Ginobili untuk keempat kalinya secara beruntun lantaran cedera, Spurs tetap tampil menggigit. Peran Ginobili bisa digantikan dengan baik oleh point guard andalan Tony Parker yang mencatat 20 poin dan 8 assist.
Kendati berlaga di depan 15.346 pendukung lawan, Spurs langsung ngebut dengan keunggulan 25-17 di kuarter pertama dan 49-35 di kuarter kedua. Namun, segalanya berubah usai jeda.
Tuan rumah 76ers sempat mengejar 49-53 walau akhirnya lagi-lagi tertinggal cukup jauh 64-71 di kuarter ketiga. Di set penentuan, 76ers kembali habis-habisan. Bahkan, mereka sempat unggul 82-75 ketika laga tinggal empat menit lagi.
Namun, sayang Evan Turner dkk. gagal mempertahankan keunggulan tersebut tdan erpaksa mesti mengakui kemenangan Spurs dengan skor 85-90. Bagi 76ers ini merupakan kekakalahan ketujuh dari sembilan pertandingan terakhir.
Sementara bagi Spurs, selain berarti kemenangan ke-33 musim ini, itu merupakan kemenangan ke-15 mereka di laga tandang, tertinggi di antara semua tim NBA. Meski demikian, Spurs masih tertahan di posisi ketiga Western Conference dengan rekor 33-11 di bawah Oklahoma City Thunder (32-9) dan LA Clippers (32-10).

This is default featured slide 1 title

This is default featured slide 2 title

This is default featured slide 3 title

This is default featured slide 4 title

This is default featured slide 5 title

Minggu, 03 Maret 2013

Algoritma Menentukan Kemungkinan Rumus Umum Sebuah Barisan

Membuat Barisan Polinom