Membuat Barisan Polinom ~ Yudha Triya Blog

Jika f sebuah fungsi polinom variabel tunggal maka barisan polinom yang dibangun dari fungsi f tersebut dapat dinyatakan dalam bentuk,

f(1) , f(2) , f(3) , .... , f(n) , .... mempunyai arti:

suku ke 1 = U₁ = f(1) suku ke 2 = U₂ = f(2) suku ke 3 = U₃ = f(3) ....................... suku ke n = U_n = f(n)	Barisan bilangan 0, 1, 3, 6, ... dapat diartikan, U₁ = 0 , U₂ = 1, U₃ = 3, U₄ = 6, .... , $U_n = \frac{1}{2} n^2 - \frac{1}{2} n$ atau barisan tersebut dibangkitkan oleh fungsi polinom $f(n) = \frac{1}{2} n^2 - \frac{1}{2} n$ berupa fungsi berderajat 2 Derajat polinom adalah pangkat tertinggi dari variabel fungsi polinom. Untuk i, a_i berupa bilangan cacah, $f(n) = a_i n^i + a_{i-1} n^{i-1} + \cdots + a_2 n^2 + a_1 n + a_0 =\sum\limits_{k=0}^{i}a_k n^k.$ maka fungsi f(n) mempunyai derajat i pada suku polinom a_inⁱ

suku ke 1 = U₁ = f(1) suku ke 2 = U₂ = f(2)
suku ke 3 = U₃ = f(3)
.......................
suku ke n = U_n = f(n)

Barisan bilangan 0, 1, 3, 6, ... dapat diartikan, U₁ = 0 , U₂ = 1, U₃ = 3, U₄ = 6, .... , $U_n = \frac{1}{2} n^2 - \frac{1}{2} n$ atau barisan tersebut dibangkitkan oleh fungsi polinom $f(n) = \frac{1}{2} n^2 - \frac{1}{2} n$ berupa fungsi berderajat 2 Derajat polinom adalah pangkat tertinggi dari variabel fungsi polinom.
Untuk i, a_i berupa bilangan cacah,

$f(n) = a_i n^i + a_{i-1} n^{i-1} + \cdots + a_2 n^2 + a_1 n + a_0 =\sum\limits_{k=0}^{i}a_k n^k.$

maka fungsi f(n) mempunyai derajat i pada suku polinom a_inⁱ

Menggali Keistimewaan Barisan Polinom

Dalam menggali keistimewaan barisan polinom kita mencoba membentuk beberapa pengertian sebagai jembatan untuk memperoleh beberapa keistimewaan tersebut.

Pengurangan Suku Barisan

Pengurangan Suku Barisan adalah hasil pengurangan suku barisan tertentu dengan suku sebelumnya. Sehingga pengurangan suku bisa dilakukan mulai suke ke dua.
Jika U_n merupakan rumus umum suku suatu barisan maka secara umum pengurangan suku dari barisan tersebut adalah U_n+1 - U_n.

Barisan Pengurangan Suku Barisan

Barisan Pengurangan Suku adalah barisan bilangan disusun dari pengurangan suku barisan suatu barisan.
Untuk mempermudah penulisan kita membuat simbol U^[i] untuk suku barisan pengurangan suku ke i.
Misalnya U_n suatu barisan maka barisan ini bukan barisan pengurangan suku dan khusus untuk ini kita sepakati sebagai U^[0]. Selanjutnya untuk n > 0,
U^[1] merupakan barisan pengurangan suku utama atau dari U sehingga U_n^[1] = U_n+1 - U_n U^[2] merupakan barisan pengurangan suku ke 1 atau dari U^[1] sehingga U_n^[2] = U_n+1^[1] - U_n^[1]
U^[3] merupakan barisan pengurangan suku ke 2 atau dari U^[2] sehingga U_n^[3] = U_n+1^[2] - U_n^[2]
...........................................
U^[i] merupakan barisan pengurangan suku ke i atau dari U^[i-1] sehingga U_n^[i] = U_n+1^[i-1] - U_n^[i-1]

Pengurangan Suku Barisan Polinom

Dengan mengambil i > 0 dan rumus umum barisan polinom,
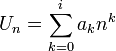
$U_n = \sum\limits_{k=0}^{i}a_k n^k$ maka Pengurangan Suku Barisan tersebut adalah
$U_{n+1} - U_n = \sum\limits_{k=0}^{i}a_k (n+1)^k - \sum\limits_{k=0}^{i}a_k (n)^k$ dengan menggunakan konsep sigma, kombinasi, dan binomial ^[3] diperoleh,
$U_{n+1} - U_n = \sum\limits_{k=0}^{i-1}a_k \sum\limits_{m=0}^{k-1} C^k_mn^m + a_i\sum\limits_{m=0}^{i-1}C^i_m n^m$

Barisan Pengurangan Suku Barisan Polinom

Dengan melihat persamaan terakhir pada pengurangan suku polinom tampak bahwa U^[1] mempunyai rumus umum sebagai berikut:
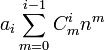
$U^{[1]}_n = \sum\limits_{k=0}^{i-1}a_k \sum\limits_{m=0}^{k-1} C^k_mn^m + a_i\sum\limits_{m=0}^{i-1}C^i_m n^m$ Tampak jelas bahwa barisan selisih suku pertama tersebut berupa barisan polinom. Derajat fungsi polinom dapat dilihat pada bagian
$a_i\sum\limits_{m=0}^{i-1}C^i_m n^m$ yaitu saat m = i-1 dan memberikan komponen polinom
$a_i C^i_{i-1} n^{i-1} = a_i i n^{i-1}$ berarti derajat fungsi polinom yang menyusun U^[1] adalah i-1 atau turun satu dari derajat fungsi polinom penyusun U. Koefisien suku fungsi polinom yang berpangkat i-1 dari penyusun U^[1] ternyata adalah koefisien suku fungsi polinom komponen yang berpangkat i dari penyusun U dikalikan derajat fungsi penyusun U atau sama dengan a_ii

Keistimewaan Barisan Polinom

Pada akhir penggalian keistimewaan barisan polinom dapat dengan mudah kita simpulkan adanya beberapa keistimawaan barisan polinom ^[4] tersebut yaitu:

Barisan selisih suku ke derajad polinom yang dibentuk akan berupa barisan konstanta.
Besar konstanta adalah ai!, dengan a koefisien suku yang berpangkat tertinggi dari fungsi yang membentuk barisan, dan i merupakan derajat fungsi polinom tersebut.

Notasi i! artinya faktorial dari i.

Minggu, 03 Maret 2013

Membuat Barisan Polinom